Quick Start guide

Hello, world!

To get started, let’s simulate a basic model and plot it. For simplicity, we will use all of the model defaults.

import matplotlib.pyplot as plt
from pyddm import Model
m = Model()
s = m.solve()
plt.plot(s.model.t_domain(), s.pdf_corr())
plt.savefig("helloworld.png")
plt.show()

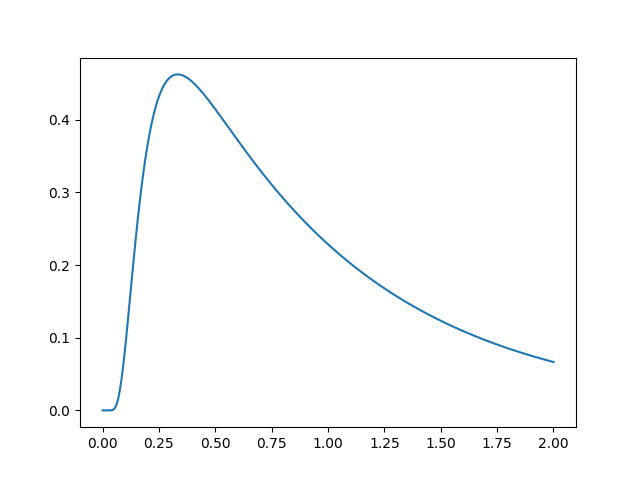
Congratulations! You’ve successfully simulated your first model! Let’s dig in a bit so that we can define more useful models.

Download this full example

Simple example

The following simulates a simple DDM with constant drift. First, it shows how to build a model and then uses it to generate artificial data. After the artificial data has been generated, it fits a new model to these data and shows that the parameters are similar.

Model is the object which represents a DDM. Its default behavior can be changed through Drift, Noise, Bound, InitialCondition, and Overlay objects, which specify the behavior of each of these model components. Each model must have one of each of these, but defaults to a simple case for each. These determine how it calculates the drift rate (Drift), diffusion coefficient (Noise), shape of the integration boundaries (Bound), initial particle distribution (InitialCondition), and any other modifications to the generated solution (Overlay).

Each of these model components may take “parameters” which are (usually) unique to that specific model component. For instance, the DriftConstant class takes the “drift” parameter, which should be passed to the constructor. Similarly, NoiseConstant takes the parameter “noise” to determine the standard deviation of the drift process, and OverlayNonDecision takes “nondectime”, the non-decision time (efferent/afferent/apparatus delay) in seconds. Some model components, such as ICPointSourceCenter which represents a starting point initial condition directly in between the bounds, does not take any parameters.

For example, the following is a DDM with drift 2.2, noise 1.5, bound 1.1, and a 100ms non-decision time. It is simulated for 2 seconds (T_dur) with reasonable timestep and grid size (dt and dx). Once we define the model, the solve() function runs the simulation. This model can be described as shown below:

from pyddm import Model
from pyddm.models import DriftConstant, NoiseConstant, BoundConstant, OverlayNonDecision, ICPointSourceCenter
from pyddm.functions import fit_adjust_model, display_model

model = Model(name='Simple model',
              drift=DriftConstant(drift=2.2),
              noise=NoiseConstant(noise=1.5),
              bound=BoundConstant(B=1.1),
              overlay=OverlayNonDecision(nondectime=.1),
              dx=.001, dt=.01, T_dur=2)
display_model(model)
sol = model.solve()

Solution objects represent correct and erred probability distribution functions over time. We can generate psuedo-data from this solved model with the resample() function:

samp = sol.resample(1000)

To fit the outputs, we first create a model with special Fittable objects in all the parameters we would like to fit. We specify the range of each of these objects as a hint to the optimizer; this is mandatory for some but not all optimization methods. Then, we run the fit_adjust_model() function, which will convert the Fittable objects to Fitted objects and find a value for each which collectively minimizes the objective function.

Here, we use the same model as above, since we know the form the model is supposed to have. We fit the model to the generated data using BIC as a loss function and differential evolution to optimize the parameters:

from pyddm import Fittable, Fitted
from pyddm.models import LossRobustBIC
from pyddm.functions import fit_adjust_model
model_fit = Model(name='Simple model (fitted)',
                  drift=DriftConstant(drift=Fittable(minval=0, maxval=4)),
                  noise=NoiseConstant(noise=Fittable(minval=.5, maxval=4)),
                  bound=BoundConstant(B=1.1),
                  overlay=OverlayNonDecision(nondectime=Fittable(minval=0, maxval=1)),
                  dx=.001, dt=.01, T_dur=2)

fit_adjust_model(samp, model_fit,
                 fitting_method="differential_evolution",
                 lossfunction=LossRobustBIC, verbose=False)

We can display the newly-fit parameters with the display_model() function:

display_model(model_fit)

This shows that the fitted value of drift is 2.2096, which is close to the value of 2.2 we used to simulate it. Similarly, noise fits to 1.539 (compared to 1.5) and nondectime (non-decision time) to 0.1193 (compared to 0.1). The fitting algorithm is stochastic, so exact values may vary slightly:

Model Simple model (fitted) information:
Drift component DriftConstant:
    constant
    Fitted parameters:
    - drift: 2.209644
Noise component NoiseConstant:
    constant
    Fitted parameters:
    - noise: 1.538976
Bound component BoundConstant:
    constant
    Fixed parameters:
    - B: 1.100000
IC component ICPointSourceCenter:
    point_source_center
    (No parameters)
Overlay component OverlayNonDecision:
    Add a non-decision by shifting the histogram
    Fitted parameters:
    - nondectime: 0.119300

While the values are close to the true values, the fit is not perfect due to the finite size of the resampled data. If we want to use these programmatically, we can use the parameters() function, like:

model_fit.parameters()

We can also draw a plot visualizing the fit. Unlike our first example, we will now use one of PyDDM’s convenience methods, plot_fit_diagnostics():

import pyddm.plot
import matplotlib.pyplot as plt
pyddm.plot.plot_fit_diagnostics(model=model_fit, sample=samp)
plt.savefig("simple-fit.png")
plt.show()

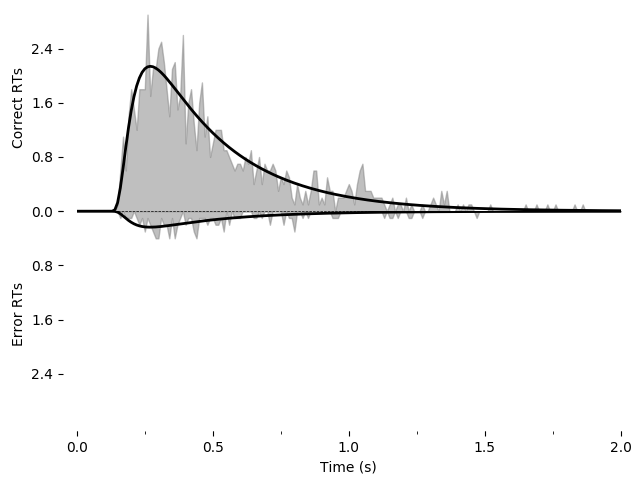
Using the Solution object sol we have access to a number of other useful functions. For instance, we can display the probability of a correct response using prob_correct() or the entire histogram of errors using pdf_err().

print(sol.prob_correct())
print(sol.pdf_err())

See the Solution object documentation for more such functions.

To save the model for later use, we can use the repr() function built-in to Python. This function outputs a string with all the information needed to recreate the object. It is very similar to the print() function, except it saves the result as a string rather than displaying it. To save, do the following:

with open("model.txt", "w") as f:
    f.write(repr(model_fit))

Then, you can load the saved model with the following. You may need to add additional imports from PyDDM if you get an “import error”.

from pyddm import FitResult
with open("model.txt", "r") as f:
    model_loaded = eval(f.read())

If you would like to just access the parameters for a separate analysis, you can save them with get_model_parameters(). The names of these parameters can be accessed with get_model_parameter_names(). Note that any “Fitted” value can be used as if it is a number/float. (It is actually a subclass of “float”!)

Download this full example

Working with data

(View a shortened interactive version of this tutorial.)

Loading data from a CSV file

In this example, we load data from the open dataset by Roitman and Shadlen (2002). This dataset can be downloaded here and the relevant data extracted with our script. The processed CSV file can be downloaded directly.

The CSV file generated from this looks like the following:

monkey	rt	coh	correct	trgchoice
1	0.355	0.512	1.0	2.0
1	0.359	0.256	1.0	1.0
1	0.525	0.128	1.0	1.0

It is fairly easy then to load and process the CSV file:

from pyddm import Sample
import pandas
with open("roitman_rts.csv", "r") as f:
    df_rt = pandas.read_csv(f)

df_rt = df_rt[df_rt["monkey"] == 1] # Only monkey 1
  
# Remove short and long RTs, as in 10.1523/JNEUROSCI.4684-04.2005.
# This is not strictly necessary, but is performed here for
# compatibility with this study.
df_rt = df_rt[df_rt["rt"] > .1] # Remove trials less than 100ms
df_rt = df_rt[df_rt["rt"] < 1.65] # Remove trials greater than 1650ms
  
# Create a sample object from our data.  This is the standard input
# format for fitting procedures.  Since RT and correct/error are
# both mandatory columns, their names are specified by command line
# arguments.
roitman_sample = Sample.from_pandas_dataframe(df_rt, rt_column_name="rt", correct_column_name="correct")

This gives an output sample with the conditions “monkey”, “coh”, and “trgchoice”.

Note that this examples requires pandas to be installed.

Loading data from a numpy array

Data can also be loaded from a numpy array. For example, let’s load the above data without first loading it into pandas:

from pyddm import Sample
import numpy as np
with open("roitman_rts.csv", "r") as f:
    M = np.loadtxt(f, delimiter=",", skiprows=1)

# RT data must be the first column and correct/error must be the
# second column.
rt = M[:,1].copy() # Use .copy() because np returns a view
corr = M[:,3].copy()
monkey = M[:,0].copy()
M[:,0] = rt
M[:,1] = corr
M[:,3] = monkey

# Only monkey 1
M = M[M[:,3]==1,:]

# As before, remove longest and shortest RTs
M = M[M[:,0]>.1,:]
M = M[M[:,0]<1.65,:]
  
conditions = ["coh", "monkey", "trgchoice"]
roitman_sample2 = Sample.from_numpy_array(M, conditions)

We can confirm that these two methods of loading data produce the same results:

assert roitman_sample == roitman_sample2

Fitting a model to data

Now that we have loaded these data, we can fit a model to them. First we will fit a DDM, and then we will fit a GDDM.

First, we want to let the drift rate vary with the coherence. To do so, we must subclass Drift. Each subclass must contain a name (a short description of how drift varies), required parameters (a list of the parameters that must be passed when we initialize our subclass, i.e. parameters which are passed to the constructor), and required conditions (a list of conditions that must be present in any data when we fit data to the model). We can easily define a model that fits our needs:

import pyddm as ddm
class DriftCoherence(ddm.models.Drift):
    name = "Drift depends linearly on coherence"
    required_parameters = ["driftcoh"] # <-- Parameters we want to include in the model
    required_conditions = ["coh"] # <-- Task parameters ("conditions"). Should be the same name as in the sample.
    
    # We must always define the get_drift function, which is used to compute the instantaneous value of drift.
    def get_drift(self, conditions, **kwargs):
        return self.driftcoh * conditions['coh']

Because we are fitting with likelihood, we must include a baseline lapse rate to avoid taking the log of 0. Traditionally this is implemented with a uniform distribution, but PyDDM can also use an exponential distribution using OverlayPoissonMixture (representing a Poisson process lapse rate), as we use here. However, since we also want a non-decision time, we need to use two Overlay objects. To accomplish this, we can use an OverlayChain object. Then, we can construct a model which uses this and fit the data to the model:

from pyddm import Model, Fittable
from pyddm.functions import fit_adjust_model, display_model
from pyddm.models import NoiseConstant, BoundConstant, OverlayChain, OverlayNonDecision, OverlayPoissonMixture
model_rs = Model(name='Roitman data, drift varies with coherence',
                 drift=DriftCoherence(driftcoh=Fittable(minval=0, maxval=20)),
                 noise=NoiseConstant(noise=1),
                 bound=BoundConstant(B=Fittable(minval=.1, maxval=1.5)),
                 # Since we can only have one overlay, we use
                 # OverlayChain to string together multiple overlays.
                 # They are applied sequentially in order.  OverlayNonDecision
                 # implements a non-decision time by shifting the
                 # resulting distribution of response times by
                 # `nondectime` seconds.
                 overlay=OverlayChain(overlays=[OverlayNonDecision(nondectime=Fittable(minval=0, maxval=.4)),
                                                OverlayPoissonMixture(pmixturecoef=.02,
                                                                      rate=1)]),
                 dx=.001, dt=.01, T_dur=2)

# Fitting this will also be fast because PyDDM can automatically
# determine that DriftCoherence will allow an analytical solution.
fit_model_rs = fit_adjust_model(sample=roitman_sample, model=model_rs, verbose=False)

Finally, we can display the fit parameters with the following command:

display_model(fit_model_rs)

This gives the following output (which may vary slightly, since the fitting algorithm is stochastic):

Model Roitman data, drift varies with coherence information:
Drift component DriftCoherence:
    Drift depends linearly on coherence
    Fitted parameters:
    - driftcoh: 10.388292
Noise component NoiseConstant:
    constant
    Fixed parameters:
    - noise: 1.000000
Bound component BoundConstant:
    constant
    Fitted parameters:
    - B: 0.744209
IC component ICPointSourceCenter:
    point_source_center
    (No parameters)
Overlay component OverlayChain:
    Overlay component OverlayNonDecision:
        Add a non-decision by shifting the histogram
        Fitted parameters:
        - nondectime: 0.312433
    Overlay component OverlayPoissonMixture:
        Poisson distribution mixture model (lapse rate)
        Fixed parameters:
        - pmixturecoef: 0.020000
        - rate: 1.000000
Fit information:
    Loss function: Negative log likelihood
    Loss function value: 199.3406727870083
    Fitting method: differential_evolution
    Solver: auto
    Other properties:
        - nparams: 3
        - samplesize: 2611
        - mess: ''

Or, to access them within Python instead of printing them,

fit_model_rs.parameters()

Note that if you see “Warning: renormalizing model solution from X to 1.” for some X, this is okay as long as X is close ($<10^{-5}$ or so) to 1.0 or as long as this is seen early in the fitting procedure. If it is larger or seen towards the end of the fitting procedure, consider using smaller dx or dt in the simulation. This indicates numerical imprecision in the simulation.

Plotting the fit

We can also graphically evaluate the quality of the fit. We can plot and save a graph:

import pyddm.plot
import matplotlib.pyplot as plt
pyddm.plot.plot_fit_diagnostics(model=fit_model_rs, sample=roitman_sample)
plt.savefig("roitman-fit.png")
plt.show()

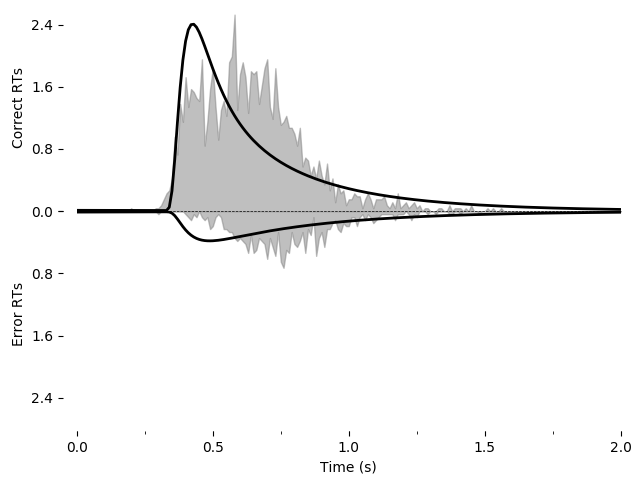
This model does not seem to fit the data very well.

We can alternatively explore this with the PyDDM’s model GUI:

pyddm.plot.model_gui(model=fit_model_rs, sample=roitman_sample)

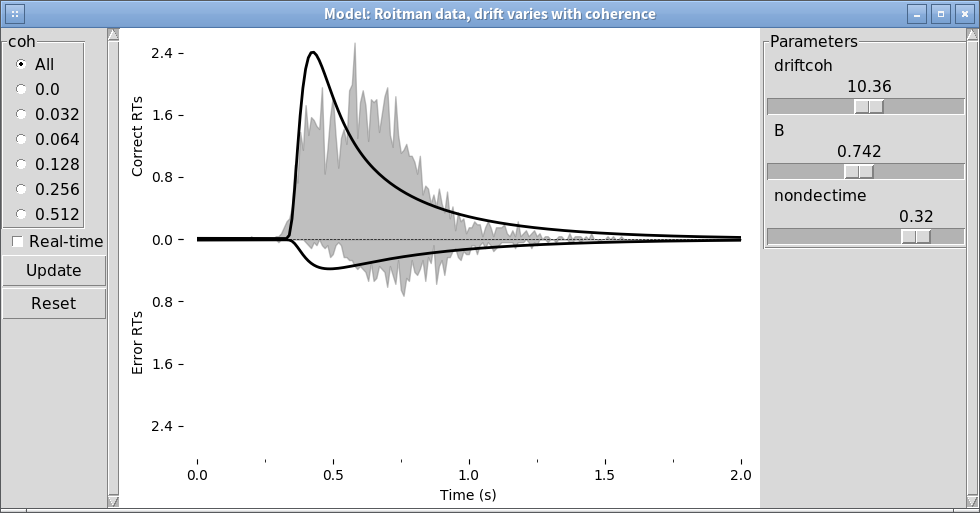
See Model GUI for more info.

Download this full example

Improving the fit

Let’s see if we can improve the fit by including additional model components. We will include exponentially collapsing bounds and use a leaky or unstable integrator instead of a perfect integrator.

To use a coherence-dependent leaky or unstable integrator, we can build a drift model which incorporates the position of the decision variable to either increase or decrease drift rate. This can be accomplished by making get_drift depend on the argument x.

class DriftCoherenceLeak(ddm.models.Drift):
    name = "Leaky drift depends linearly on coherence"
    required_parameters = ["driftcoh", "leak"] # <-- Parameters we want to include in the model
    required_conditions = ["coh"] # <-- Task parameters ("conditions"). Should be the same name as in the sample.
    
    # We must always define the get_drift function, which is used to compute the instantaneous value of drift.
    def get_drift(self, x, conditions, **kwargs):
        return self.driftcoh * conditions['coh'] + self.leak * x

Collapsing bounds are already included in PyDDM, and can be accessed with BoundCollapsingExponential.

Thus, the full model definition is

from pyddm.models import BoundCollapsingExponential
model_leak = Model(name='Roitman data, leaky drift varies with coherence',
                   drift=DriftCoherenceLeak(driftcoh=Fittable(minval=0, maxval=20),
                                            leak=Fittable(minval=-10, maxval=10)),
                   noise=NoiseConstant(noise=1),
                   bound=BoundCollapsingExponential(B=Fittable(minval=0.5, maxval=3),
                                                    tau=Fittable(minval=.0001, maxval=5)),
                   # Since we can only have one overlay, we use
                   # OverlayChain to string together multiple overlays.
                   # They are applied sequentially in order.  OverlayDelay
                   # implements a non-decision time by shifting the
                   # resulting distribution of response times by
                   # `delaytime` seconds.
                   overlay=OverlayChain(overlays=[OverlayNonDecision(nondectime=Fittable(minval=0, maxval=.4)),
                                                  OverlayPoissonMixture(pmixturecoef=.02,
                                                                        rate=1)]),
                   dx=.01, dt=.01, T_dur=2)

Before fitting this model, let’s look at it in the model GUI:

from pyddm.plot import model_gui
model_gui(model_leak, sample=roitman_sample)

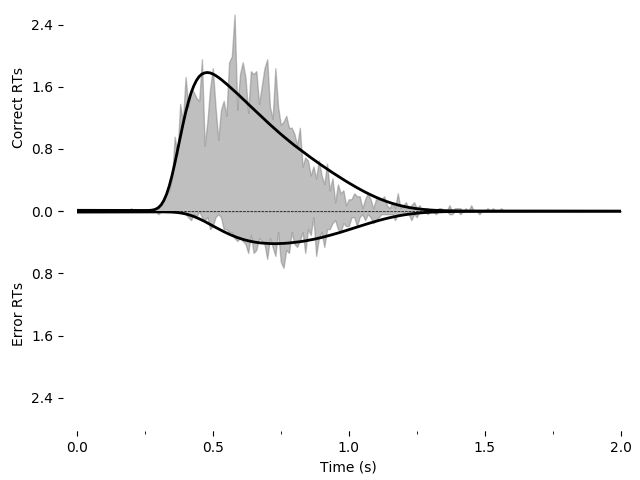
We can fit this and save it as an image using the following. Note that this may take a while (hours) due to the increased number of parameters and because the earlier examples were able to use the analytical solver but the present example must use backward Euler. For all coherences, the fit is:

fit_model_leak = fit_adjust_model(sample=roitman_sample, model=model_leak, verbose=False)
pyddm.plot.plot_fit_diagnostics(model=fit_model_leak, sample=roitman_sample)
plt.savefig("leak-collapse-fit.png")

Going further

Just as we created DriftCoherence above (by inheriting from Drift) to modify the drift rate based on coherence, we can modify other portions of the model. See PyDDM Cookbook for more examples. Also see the API Documentation for more specific details about overloading classes.

Summary

PyDDM can simulate models and generate artificial data, or it can fit them to data. Below are high-level overviews for how to accomplish each.

To simulate models and generate artificial data:

1. Optionally, define unique components of your model. Models are modular, and allow specifying a dynamic drift rate, noise level, diffusion bounds, starting position of the integrator, or post-simulation modifications to the RT histogram. Many common models for these are included by default, but for advance functionality you may need to subclass Drift, Noise, Bound, InitialCondition, or Overlay. These model components may depend on “conditions”, i.e. prespecified values associated with the behavioral task which change from trial to trial (e.g. stimulus coherence), or “parameters”, i.e. values which apply to all trials and should be fit to the subject.
2. Define a model. Models are represented by creating an instance of the Model class, and specifying the model components to use for it. These model component can either be the model components included in PyDDM or ones you created in step 1. Values must be specified for all parameters required by model components.
3. Simulate the model using the Model.solve() method to generate a Solution object. If you have multiple conditions, you must run Model.solve() separately for each set of conditions and generate separate Solution objects.
4. Run the Solution.resample() method of the Solution object to generate a Sample. If you have multiple Solution objects (for multiple task conditions), you will need to generate multiple Sample objects as well. These can be added together with the “+” operator to form one single Sample object.

To fit a model to data:

1. Optionally define unique components of your model, as mentioned in Step 1 above.
2. Load your data into a Sample object using either Sample.from_numpy_array() or Sample.from_pandas_dataframe(). If you have multiple task conditions (i.e. prespecified values associated with the behavioral task which change from trial to trial), make sure that the names of the conditions in the Sample object align with those that are used in your model components. (In other words, if a model component expects a coherence value named “coh”, make sure your sample includes a coherence value named “coh”.)
3. Define a model. Models are represented by creating an instance of the Model class, and specifying the model components to use for it. These model component can either be the model components included in PyDDM or ones you created in step 1. Parameters for the model components must either be specified expicitly or else set to a Fittable instance, for example “Fittable(minval=0, maxval=1)”.

3. Run fit_adjust_model() on the model and the sample. Optionally specify a loss function other than the default (which uses BIC). After fitting, the Fittable objects in the model will be changed to Fitted objects, which are just like Fittable objects except they contain the fitted values.
4. View the output by calling display_model() on the model. The value of the loss function is accessible via Model.get_fit_result().