How-to guides¶
Parallelization¶
PyDDM has built-in support for parallelization if pathos is installed.
To use parallelization, first set up the parallel pool:
from pyddm import set_N_cpus
set_N_cpus(4)
Then, PyDDM will automatically parallelize the fitting routines. For example, just call:
fit_model_rs = fit_adjust_model(sample=roitman_sample, model=model_rs)
There are a few caveats with parallelization:
- It is only possible to run fits in parallel if they are on the same computer. It is not possible to fit across multiple nodes in a cluster, for example.
- Due to a bug in pathos, all model components must be defined in a separate file and then imported.
- Only models with many conditions will be sped up by
parallelization. The cardinality of the cartesian product of the
conditions is the maximum number of CPUs that will have an effect:
for example, if you have four coherence conditions, a right vs left
condition, and a high vs low reward condition, then after
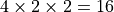 CPUs, there will be no benefit to
increasing the number of CPUs.
CPUs, there will be no benefit to
increasing the number of CPUs. - It is possible but not recommended to set the number of CPUs to be greater than the number of physical CPU cores on the machine. This will cause a slight reduction in performance.
Fitting models with custom algorithms¶
As described in fit_adjust_model(), three different algorithms
can be used to fit models. The default is differential evolution,
which we have observed to be robust for models with large numbers of
parameters.
Other methods can be used by passing the “fitting_method” argument to
fit_adjust_model() or fit_model(). This can take one of
several values:
- “simplex”: Use the Nelder-Mead simplex method
- “simple”: Gradient descent
- “basin”: Use Scipy’s basin hopping algorithm.
- A function can be passed to use this function as a custom objective function.
For example, to fit the model in the quickstart using the Nelder-Mead simplex method, you can do:
fit_model_rs = fit_adjust_model(sample=roitman_sample, model=model_rs, fitting_method="simplex")
Retrieve the evolving pdf of a solution¶
Setting return_evolution=True in solve_numerical() will (with methods “implicit” and “explicit” only) return an M-by-N array (as part of the Solution) whose columns contain the cross-sectional pdf for every time step:
sol = model.solve_numerical_implicit(conditions=conditions, return_evolution=True)
sol.pdf_evolution()
This is equivalent to (but much faster than):
sol = np.zeros((len(model.x_domain(conditions)), len(model.t_domain())))
sol[:,0] = model.IC(conditions=conditions)/model.dx
for t_ind, t in enumerate(model.t_domain()[1:]):
T_dur_backup = model.T_dur
model.T_dur = t
ans = model.solve_numerical_implicit(conditions=conditions, return_evolution=False)
model.T_dur = T_dur_backup
sol[:,t_ind+1] = ans.pdf_undec()
Note that:
sum(pdf("correct")[0:t]*dt) + sum(pdf("error")[0:t]*dt) + sum(pdf_evolution()[:,t]*dx) = 1
Stimulus coding vs accuracy coding vs anything else coding¶
By default, the upper boundary in PyDDM represents “correct” choices and the lower boundary represents “error” choices. However, these boundaries can represent whatever you would like: “left” vs “right” choice, “high value” vs “low value” choice, choice “inside the receptive field” vs “outside the receptive field”, etc.
To change the name of the choices represented by the bounds, we need to pass the name of the two boundaries as an argument to the Model and the Sample. For example, if “High value” is represented by the upper boundary and “Low value” by the lower boundary, we can write:
model = Model(..., choice_names=("High value", "Low value"))
sample = Sample.from_pandas_dataframe(..., choice_names=("High value", "Low value"))
Then, these names can be used to access properties of sample or solution from the solved model, just as we did for “correct” and “error” in the tutorial. For example:
sample.prob("High value")
sol = model.solve()
sol.prob("High value")
sol.pdf("Low value")
However, note that the data must be in the appropriate format. You are responsible for formatting the data correctly for these interpretations to hold. For example, consider the Roitman-Shadlen dataset from the tutorial. The dataset looks as follows:
| monkey | rt | coh | correct | trgchoice |
|---|---|---|---|---|
| 1 | 0.355 | 0.512 | 1.0 | 2.0 |
| 1 | 0.359 | 0.256 | 1.0 | 1.0 |
| 1 | 0.525 | 0.128 | 1.0 | 1.0 |
In this format, “coh” is the motion coherence, “correct” is whether the monkey chose the target in the direction of the random dot motion, and “trgchoice” is whether the monkey chose target 1 (inside the receptive field) or target 2 (outside the receptive field). In this experiment, the targets were chosen to be in different places for each session, so they did not map directly onto a location on the screen.
Let’s make the top boundary represent “target 1” and the bottom represent “target 2”. We already have the variable “trgchoice”, describing whether the monkey chose “target 1” or “target 2”. So we can use this as the “choice” variable (for which we previously used “correct” or “error”). PyDDM assumes that the upper boundary choice is given by a “1” and the lower boundary choice by “0”, so all we need to correct the trgchoice variable such that responses to target 2 are coded as “0” instead of “2”.
But, the “coh” column measures coherence with respect to the correct choice, not
with respect to one of the targets. Since we are defining our upper boundary
choice as “target 1” and our lower boundary choice as “target 2”, positive
coherence should represent the case where the stimulus showed motion in the
direction of “target 1” and negative coherence in the direction of “target 2”.
In the dataset, “coh” is always positive. So, we need to make “coh” negative if
the motion was coherent towards “target 2”. This happened when the monkey was
correct and chose target 2 (correct == 1.0 and trgchoice == 2.0) or when the
monkey was incorrect and chose target 1 (correct == 0.0 and trgchoice ==
1.0).
So, after performing these transformations, our dataset looks like the following:
| monkey | rt | coh | correct | choice |
|---|---|---|---|---|
| 1 | 0.355 | -0.512 | 1.0 | 0.0 |
| 1 | 0.359 | 0.256 | 1.0 | 1.0 |
| 1 | 0.525 | 0.128 | 1.0 | 1.0 |
Loading the data therefore looks like:
# Read the dataset into a Pandas DataFrame
from pyddm import Sample
import pandas
with open("roitman_rts.csv", "r") as f:
df_rt = pandas.read_csv(f)
df_rt = df_rt[df_rt["monkey"] == 1] # Only monkey 1
# Remove short and long RTs, as in 10.1523/JNEUROSCI.4684-04.2005.
# This is not strictly necessary, but is performed here for
# compatibility with this study.
df_rt = df_rt[df_rt["rt"] > .1] # Remove trials less than 100ms
df_rt = df_rt[df_rt["rt"] < 1.65] # Remove trials greater than 1650ms
# Adjust the dataset for stimulus coding
df_rt['choice'] = df_rt['trgchoice'] % 2
df_rt['coh'] = df_rt['coh'] * ((df_rt["choice"] == df_rt["correct"])*2-1)
# Create a sample object from our data. This is the standard input
# format for fitting procedures. Since RT and correct/error are
# both mandatory columns, their names are specified by command line
# arguments.
roitman_sample = Sample.from_pandas_dataframe(df_rt, rt_column_name="rt", choice_column_name="choice", choice_names=("target 1", "target 2"))
And defining and fitting the model looks like:
# Define a model which uses our new DriftCoherence defined above.
from pyddm import Model, Fittable
from pyddm.functions import fit_adjust_model, display_model
from pyddm.models import NoiseConstant, BoundConstant, OverlayChain, OverlayNonDecision, OverlayPoissonMixture
model_rs = Model(name='Roitman data, drift varies with coherence',
drift=DriftCoherence(driftcoh=Fittable(minval=-20, maxval=20)),
noise=NoiseConstant(noise=1),
bound=BoundConstant(B=Fittable(minval=.1, maxval=1.5)),
# Since we can only have one overlay, we use
# OverlayChain to string together multiple overlays.
# They are applied sequentially in order. OverlayNonDecision
# implements a non-decision time by shifting the
# resulting distribution of response times by
# `nondectime` seconds.
overlay=OverlayChain(overlays=[OverlayNonDecision(nondectime=Fittable(minval=0, maxval=.4)),
OverlayPoissonMixture(pmixturecoef=.02,
rate=1)]),
choice_names=("target 1", "target 2"),
dx=.001, dt=.01, T_dur=2)
# Fitting this will also be fast because PyDDM can automatically
# determine that DriftCoherence will allow an analytical solution.
fit_model_rs = fit_adjust_model(sample=roitman_sample, model=model_rs, verbose=False)
display_model(fit_model_rs)
fit_model_rs.parameters()
As we see, we recover approximately the same parameters:
Model Roitman data, drift varies with coherence information:
Choices: 'target 1' (upper boundary), 'target 2' (lower boundary)
Drift component DriftCoherence:
Drift depends linearly on coherence
Fitted parameters:
- driftcoh: 10.362975
Noise component NoiseConstant:
constant
Fixed parameters:
- noise: 1.000000
Bound component BoundConstant:
constant
Fitted parameters:
- B: 0.744039
IC component ICPointSourceCenter:
point_source_center
(No parameters)
Overlay component OverlayChain:
Overlay component OverlayNonDecision:
Add a non-decision by shifting the histogram
Fitted parameters:
- nondectime: 0.310893
Overlay component OverlayPoissonMixture:
Poisson distribution mixture model (lapse rate)
Fixed parameters:
- pmixturecoef: 0.020000
- rate: 1.000000
Fit information:
Loss function: Negative log likelihood
Loss function value: 199.33386049405675
Fitting method: differential_evolution
Solver: auto
Other properties:
- nparams: 3
- samplesize: 2611
- mess: ''
When displaying in the model GUI, as desired, the two distributions represent “target 1” and “target 2” instead of “correct” and “error”.
pyddm.plot.model_gui(model=fit_model_rs, sample=roitman_sample)
This coding scheme may impact the interpretation of the other parameters in the model, so be careful! For example, starting point biases require special considerations.